Car Seating
2009-03-18
We have 19 people going on spring break, including myself. I've been thinking about how to organize people in the three vans, and came up with this:
A legend is available, although I did not show the single arrow relations... :D
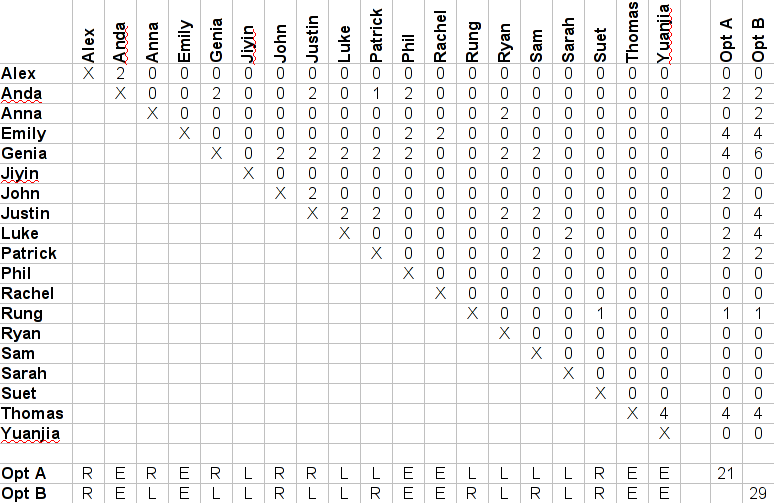
The problem is that only the people in blue and red are drivers, and the people in red each own one of the vans (and therefore must be in separate cars). The drivers should split evenly between the three cars. I also tried to maintain the male:female ratio in each car.
I assigned points to the relationships (1 to acquaintances, 2 to friends, 4 to boy/girl friends), and derived this:
Clearly the current solution is better than the old one (by a whole 8 points!).
This problem is NP-complete, and while I could write an algorithm to exhaustively search the space of possible allocations,
- It's probably tedious, especially with the male:female constraints
- I don't feel like it
- I think this is a near optimal solution (read: good enough).
It's rather amazing how the human eye can so quickly form a near optimal solution, while a computer has to calculate the points for each configuration separately.
I am open to better solutions.